Combination of Resistor

-


SERIES CIRCUIT

  यदि दो या दो से अधिक घटक श्रृंखला में जुड़े होते हैं तो उनके अंत में धारा (current) समान होता है।
    सीरीज़ सर्किट को कभी-कभी Current-coupled  या Daisy chain-coupled  कहा जाता है।
    
                            एक श्रृंखला सर्किट की सिद्धांत विशेषता यह है कि इसमें केवल एक ही पथ है जिसमें धारा प्रवाह हो सकता है। किसी भी बिंदु पर एक श्रृंखला सर्किट खोलना या तोड़ना पूरे सर्किट को "खोलने" या संचालन बंद कर देता है। उदाहरण के लिए, यदि क्रिसमस के पेड़ की रोशनी की पुरानी शैली की स्ट्रिंग में प्रकाश बल्बों में से एक भी जलता है या हटा दिया जाता है, तो बल्ब बदल जाने तक पूरी स्ट्रिंग निष्क्रिय हो जाती है।


Voltage

   In a series circuit the voltage is addition of all the voltage elements.

{\displaystyle V=V_{1}+V_{2}+V_{3}+\dots +V_{n}}


CUrrent

       {\displaystyle I=I_{1}=I_{2}=I_{3}=\cdots =I_{n}}

👉 In a series circuit, the current is the same for all of the elements.

Resistors


The total resistance of resistors in series is equal to the sum of their individual resistances:-
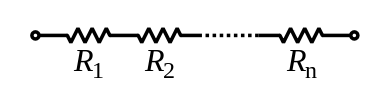
                     This is a diagram of several resistors, connected end to end, with the same amount of current through each.
                 
    {\displaystyle R_{\text{total}}=R_{1}+R_{2}+\cdots +R_{n}}

Inductors

                   Inductors follow the same law, in that the total inductance of non-coupled inductors in series is equal to the sum of their individual inductances:

                 A diagram of several inductors, connected end to end, with the same amount of current going through each.
 L_\mathrm{total} = L_1 + L_2 + \cdots + L_n


Capacitors


Capacitors follow the same law using the reciprocals. The total capacitance of capacitors in series is equal to the reciprocal of the sum of the reciprocals of their individual capacitances:

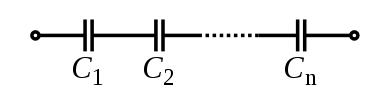
               A diagram of several capacitors, connected end to end, with the same amount of current going through each.
 
  \frac{1}{C_\mathrm{total}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}

PARALLEL CIRCUIT 


                           यदि दो या दो से अधिक घटक समानांतर में जुड़े होते हैं तो उनके अंत में Potential difference (वोल्टेज) समान होता है। घटकों में संभावित मतभेद समानता में समान हैं, और उनके समान समान ध्रुवीयताएं भी हैं। समान वोल्टेज समानांतर में जुड़े सभी सर्किट घटकों पर लागू होता है। Kirchhoff's Law के अनुसार, कुल वर्तमान विशिष्ट घटकों के माध्यम से धाराओं का योग है।

Voltage
समानांतर सर्किट में वोल्टेज सभी तत्वों के लिए समान होता है।
             
                      V = V_1 = V_2 = \ldots = V_n

CUrrent
प्रत्येक विशिष्ट प्रतिरोधी में धारा Ohm's law द्वारा पाया जाता है।
                        Factoring out the voltage gives

               I_\mathrm{total} = V\left(\frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}\right)

Resistors


To find the total resistance of all components, add the reciprocals of the resistances  of each component and take the reciprocal of the sum. Total resistance will always be less than the value of the smallest resistance:

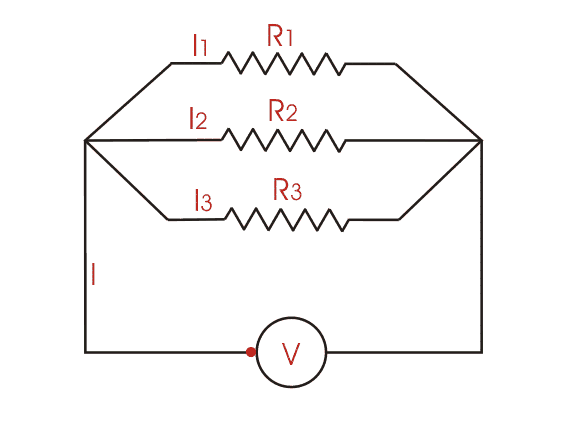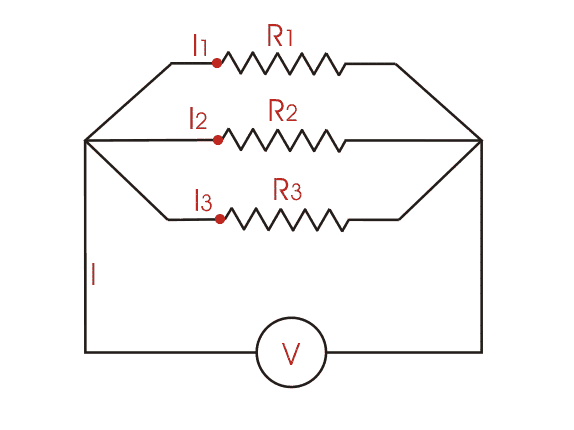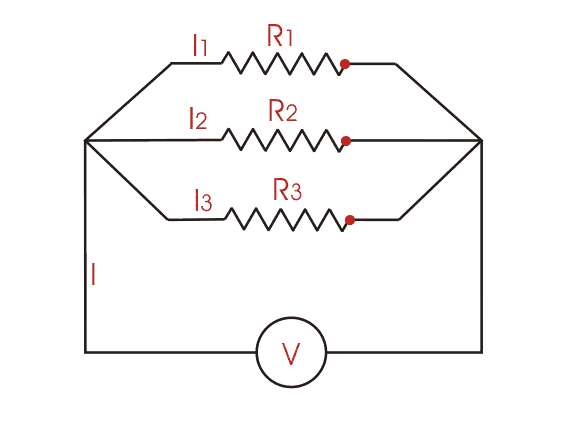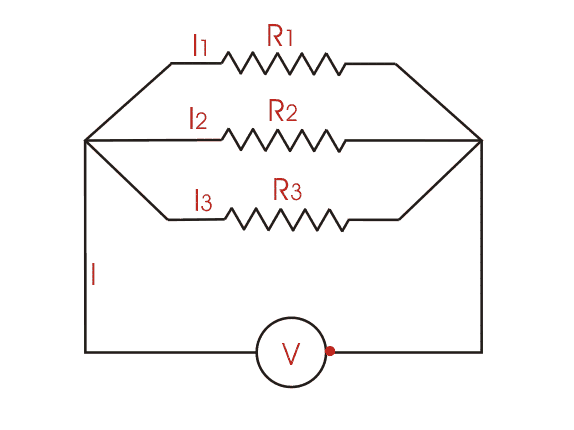
                 Combination of three resistors in parallel

                  \frac{1}{R_\mathrm{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n}

For only two resistors, the unreciprocated expression is reasonably simple:

                        {\displaystyle R_{\mathrm {total} }={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}.}

Inductors


 Inductors follow the same law, in that the total inductance of non-coupled inductors in parallel is equal to the reciprocal of the sum of the reciprocals of their individual inductances:

          A diagram of several inductors, side by side, both leads of each connected to the same wires.

                  \frac{1}{L_\mathrm{total}} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n}

Capacitors


The total capacitance of capacitors in parallel is equal to the sum of their individual capacitances:

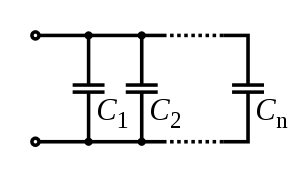
              A diagram of several capacitors, side by side, both leads of each connected to the same wires.

                        C_\mathrm{total} = C_1 + C_2 + \cdots + C_n


DIFFRENCE Btw. SERIES & PARALLEL CIRCUIT

Series Circuits

PARALLEL CIRCUITS
All components share the same (equal) current.
All components share the same (equal) voltage.
Voltage drops add to equal total voltage.
Branch currents add to equal total current.
Resistances add to equal total resistance.
Resistances diminish to equal total resistance.





Comments

Post a Comment

Popular posts from this blog

Basic Thermodynamics

-
Image
THERMODYNAMICS Combination of two greek word  Therme(Heat) and Dynamis(Power) Thermodynamic System :- Thermodynamic system is defined as Quantity of matter or a region in space on which our study is focused. THERMO-D SYSTEM 1. Closed System  2. Open System  3. Isolated System SURROUNDING Anything that is external to system that is known as Surrounding. BOUNDARY A real or imaginary surface which separate system and Surrounding that surface known as Boundary. ☀ Mathematically boundary has not thickness. ☀ The volume of boundary its self is zero. ☀ Boundary could be fixed or imaginary. CLOSED SYSTEM ☀ Closed System is nothing but a control mass.   Mass can not cross system boundary But Energy can cross the system boundary. OPEN SYSTEM ☀ Mass as well as energy interaction.  Mass and Energy both can transfer or cross the system boundary. ISOLATED SYSTEM There is no mass and energy transfer across the boundary. PROCESS Continuous change of state. ⓵ Reversi...
Read more

Classical Mechanics

-
Image
👉Classical Mechanics also known as Classical Physics Classical mechanics deals with the motion of bodies under the influence of forces or with the equilibrium of bodies when all forces are balanced. The subject may be thought of as the elaboration and application of basic postulates first enunciated by Isaac Newton in his Philosophiae Naturalis Principia Mathematica (1687), commonly known as the Principia. These postulates, called Newton’s laws of motion, are set forth below. They may be used to predict with great precision a wide variety of phenomena ranging from the motion of individual particles to the interactions of highly complex systems.                             The central concepts in classical mechanics are force, mass, and motion. Neither force nor mass is very clearly defined by Newton, and both have been the subject of much philosophical speculation since Newton. Both of them are best known by their e...
Read more

Mendel's Law of Segregation

-
Image
                                                                                                          The principal of Segregation is also known as Mendel's first Law.                             पृथक्करण के कानून (Law of Segregation) में कहा गया है कि प्रत्येक व्यक्तिगत जीव में प्रत्येक विशेषता के लिए दो एलील होते हैं, और ये एलील अलग-अलग (अलग) मेयोइसिस के दौरान होते हैं जैसे कि प्रत्येक गैमेटे में केवल एक ही एलील होता है। इस प्रकार एक संतान को माता-पिता जीवों से समरूप गुणसूत्रों को विरासत में प्राप्त करके एक विशेषता के लिए एलील की एक जोड़ी प्राप्त होती है: प्रत्येक माता-पिता से प्रत्येक विशेषता के लिए एक एलील।     ...
Read more